Which of the following integrals computes the area below? (See image)
![![enter image source here]]() (
(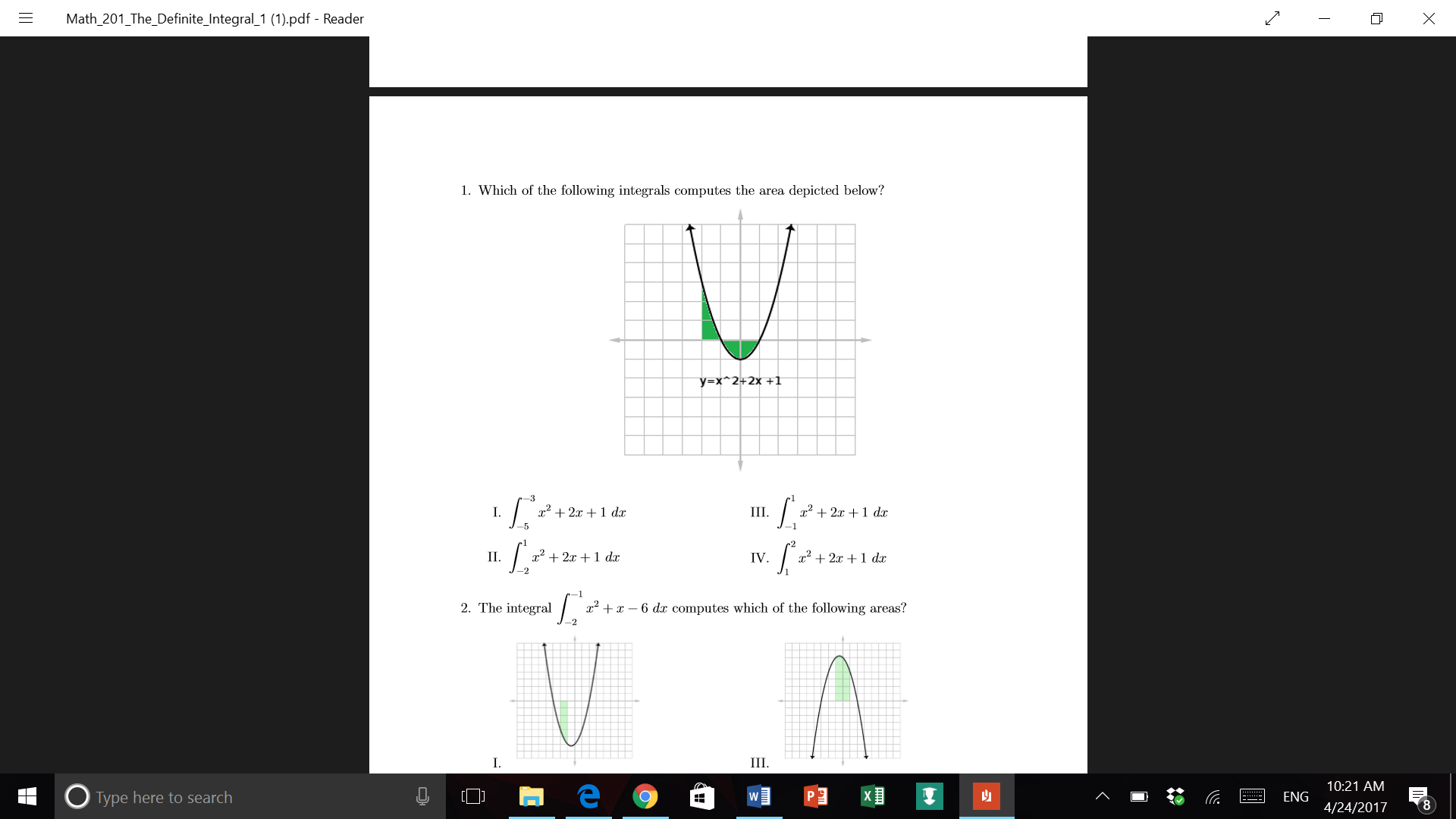 )
)
(
 )
)
2 Answers
I really don't like this question but I am led to believe the answer is
Explanation:
The answer cannot be
The answer cannot be
The answer cannot be
The reason I do not like the question is that you cannot evaluate positive and negative areas in the same integral.
As such you have to split the region and take the absolute value of the negative region.
So the interval we are looking for is
Breaking this into two parts gives us
Now we can combine this
Simplify
It has been a long time since my Fundamental Theorem of Calculus lectures!
Do we feel the graph should look like this?
Explanation:
Please comment

