Given #f(x)=x^2-3x+(3x^3)/(x-7)# at #x=2#
let us solve for the point #(x_1, y_1)# first
#f(x)=x^2-3x+(3x^3)/(x-7)#
At #x=2#
#f(2)=(2)^2-3(2)+(3(2)^3)/(2-7)#
#f(2)=4-6+24/(-5)#
#f(2)=(-10-24)/5#
#f(2)=-34/5#
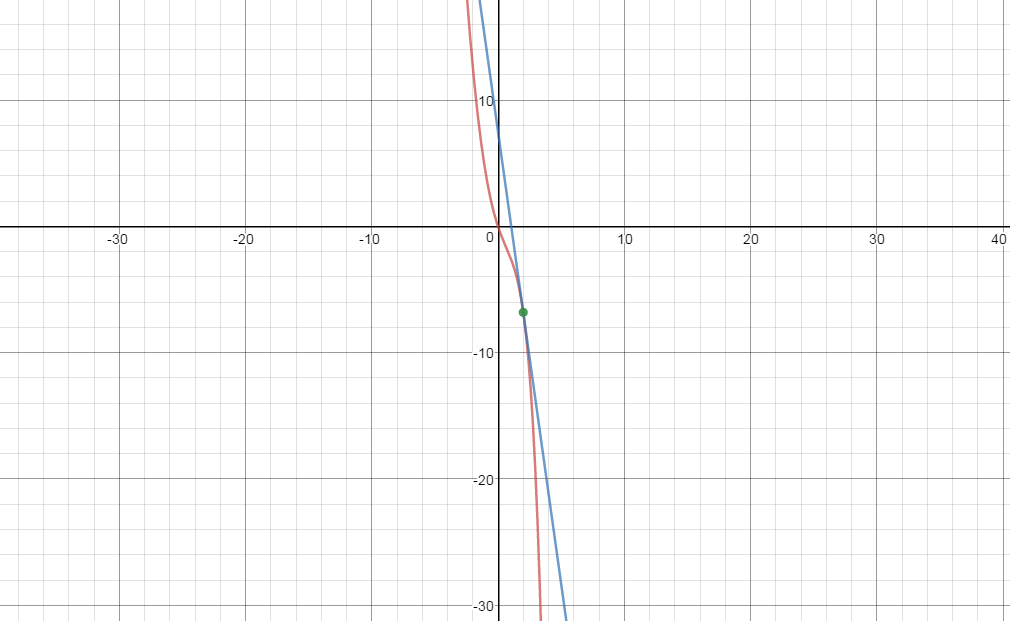
#(x_1, y_1)=(2, -34/5)#
Let us compute for the slope by derivatives
#f(x)=x^2-3x+(3x^3)/(x-7)#
#f' (x)=2x-3+((x-7)*9x^2-(3x^3)*1)/(x-7)^2#
Slope #m=f' (2)=2(2)-3+((2-7)*9(2)^2-(3(2)^3)*1)/(2-7)^2#
#m=4-3+(-180-24)/25#
#m=1-204/25=-179/25#
The equation of the Tangent line by Point-Slope Form
#y-y_1=m(x-x_1)#
#y-(-34/5)=-179/25(x-2)#
#y+34/5=-179/25(x-2)#
#25y+170=-179(x-2)#
#25y+170=-179x+358#
#179x+25y=188#
Kindly see the graph of #f(x)=x^2-3x+(3x^3)/(x-7)# and #179x+25y=188#
 )
)
God bless....I hope the explanation is useful.
 )
) 