How do you find the vertex, focus and directrix of # x^2-4x+y+3=0#?

Question

4672 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-21T05:23:59

Vertex #(2,1)#

Focus #(2,3/4)#

Directrix #y = 5/4#

Complete the square.

#y = -x^2 + 4x -3#

#= -(x -2)^2 + 1#

The vertex is at #(2,1)#.

The parabola is concave down, as the leading coefficient

#a = -1 < 0#

graph{-x^2+4x-3 [-10, 10, -5, 5]}

Therefore, the focus lies #p = 1/(4abs(a))# below the vertex.

#p = frac{1}{4abs(-1)} = 1/4#

The #y#-coordinate of the focus is #1 - 1/4 = 3/4#.

The coordinates of the focus is #(2,3/4)#.

All points on the parabola are equidistant from the focus and the perpendicular to the directrix.

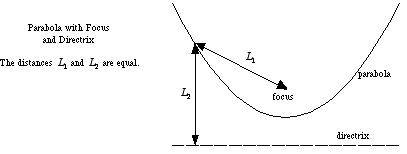
www.mathwords.com

We know that the directrix is a horizontal line, with the equation #y = m#, where #m# is the constant to be determined.

We consider the distance of the vertex to the focus, it is #p = 1/4#. Therefore, the directrix is a horizontal line #1/4# above the vertex #(2,1)#.

#m = 1 + 1/4 = 5/4#

The equation of the directrix is #y = 5/4#.