#sf(""^24Na)# undergoes #beta# decay. A 208g sample decays such that 13g remain. What is the 1/2 life ?

If we begin with 208 grams at the end of 1 half-life there would be 104 grams remaining, at the end of the 2nd half-life there would be 52 grams, at the end of the 3rd half-life there would be 26 grams and at the end of the 4th half-life there would be 13 grams.

The total time of decay is 60 hours and this represents 4 half-lifes.

#(60 hours)/(4 half-lifes) = 15 hours/half-life

The half-life for Sodium-24 is 15 hours.

The above answer is a good answer for that specific question so I will give an answer for a more general situation where the numbers may not work out so nicely.

For a random event such as the decay of a radioactive nucleus the rate of decay depends only on the number of undecayed atoms.

#RatepropN#

We replace the proportional sign by a constant , in this case the Greek letter lambda #lambda#.

Since the number of atoms is decreasing we can write:

#Rate=-lambdaN#

#lambda# is called the decay constant and is a measure of how quickly the isotope is decaying.

You may have seen the same thing if you have studied 1st order reaction kinetics - the theory is just the same and applies to many natural processes referred to as "exponential decay". #lambda# is directly analogous to the rate constant k in chemical kinetics.

A typical decay curve looks like this:

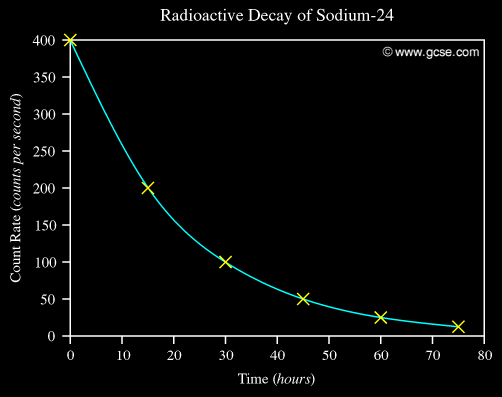
By doing some mathematics using integration (which I won't go into here) we get:

#N_t=N_0e^(-lambdat)#

#N_t# are the number of undecayed atoms at time t
#N_0# are the initial number of atoms
#lambda# is the decay constant which I described earlier
#t# is the time elapsed.

To turn this expression into a more usable form we take natural logs of both sides to give:

#lnN_t=lnN_0-lambdat#

So

#lnN_t-lnN_0=-lambdat#

#rArr#

#ln((N_t)/(N_0))=-lambdat#

We can use mass in grams for numbers of atoms (since they are proportional) so we can put in the numbers to get #lambda#:

#ln((13)/(208))=-lambda*60#

#-2.77=-lambda*60#

#lambda = 0.046 s^(-1)#

The faster the decay (related to #lambda#), the shorter the half - life. The relation between the two is given by this expression (again I won't bother you with the derivation):

#t_(1/2)=0.693/lambda#

So:

#t_(1/2)=0.693/0.046=15s#

So you can use a particular value of #N_t# and #N_0# to get #lambda# and hence #t_(1/2)#.