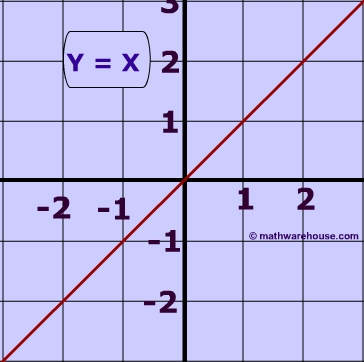
The range of a function is all possible output, or #y#, values. The domain is all possible input, or #x#, values. In the case of #y=x#, both the range and domain are all real numbers.You can plug in all sorts of negative and positive #x# and #y# values; there are no restrictions. So, in interval notation
The range: (-∞, ∞)
The domain: (-∞, ∞)
Note the round brackets ( ) because since infinity isn't a number, the functions can't be defined there. The functions just tend to infinity as the #x# and #y# values get infinitely large or infinitely small.
The function #y=x# is an interesting case of domain and range because the domain and range values are always the same. In other words, since #y# always equals #x#, the input values always equal the output values.#y=x# is also actually just the graph of a straight line, with a slope of 1 and a #y#-intercept at (0,0). You'll see that all points will have equivalent values, so some points on the line would be (4,4) or (-178, -178). To graphically observe the equivalence of the domain and range, here is a graph of the line: